Existence of Solution for a Kind of Fractional Kirchhoff Equation with Logarithmic Nonlinearity(PDF)
《南京师大学报(自然科学版)》[ISSN:1001-4616/CN:32-1239/N]
- Issue:
- 2023年01期
- Page:
- 24-27
- Research Field:
- 数学
- Publishing date:
Info
- Title:
- Existence of Solution for a Kind of Fractional Kirchhoff Equation with Logarithmic Nonlinearity
- Author(s):
- Huang Hong1; Shang Xudong2
- (1.Zhongbei College, Nanjing Normal University, Zhenjiang 212334, China)
(2.Taizhou College, Nanjing Normal University, Taizhou 225300, China)
- Keywords:
- fractional Kirchhoff equation; logarithmic nonlinearity; compactness condition; mountain pass lemma
- PACS:
- O175.8
- DOI:
- 10.3969/j.issn.1001-4616.2023.01.005
- Abstract:
- By proving the compactness condition through careful estimation of logarithmic terms,and with the help of mountain pass lemma,the authors study the existence of nontrivial solution for a kind of fractional Kirchhoff equation with logarithmic nonlinear term
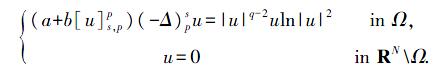
under certain conditions.
References:
[1]KIRCHHOFF G. Vorlesungen Uber Mechanik,Teubner,Leipzig[M]. Stutgarty:Springer,1883.
[2]PERERA K,ZHANG Z. Nontrivial solutions of Kirchhoff-type problems via the Yang index[J]. Journal of differential equations,2006,221:246-255.
[3]CHEN C Y,KUO Y C,WU T F. The Nehari manifold for a Kirchhoff type problem involving sign-changing weight functions[J]. Journal of differential equations,2011,250:1876-1908.
[4]FISCELLA A,VALDINOCI E. A critical Kirchhoff type problem involving a nonlocal operator[J]. Nonlinear analysis,2014,94:156-170.
[5]PUCCI P,XIANG M Q,ZHANG B L. Existence of entire solutions for Kirchhoff type equations involving the fractional p-Laplacian[J]. Advances in nonlinear analysis,2016,5:27-55.
[6]XIANG M Q,PUCCI P,SQUASSINA M,et al. Nonlocal Schr?inger Kirchhoff equations with external magnetic field[J]. Discrete and continuous dynamical systems,2017,37:503-521.
[7]SONG Y Q,SHI S Y. Existence of infinitely many solutions for degenerate p-fractional Kirchhoff equations with critical Sobolev-Hardy nonlinearities[J]. Zeitschrift fur angewandte mathematik und physik,2017,68:1-13.
[8]D’AVENIA P,SQUASSINA M,ZENARI M. Fractional logarithmic Schr?inger equations[J]. Mathematical methods in the applied sciences,2015,38:5207-5216.
[9]TRUONG L X. The Nehari manifold for fractional p-Laplacian equation with logarithmic nonlinearity on whole space[J]. Computers and mathematics with applications,2019,78:3931-3940.
[10]DI NEZZA E,PALATUCCI G,VALDINOCI E. Hitchhiker’s guide to the fractional Sobolev spaces[J]. Bulletin des sciences mathématiques,2012,136:521-573.
[11]RABINOWITZ P H. Minimax methods in critical point theory with applications to diferential equations[M]. Providence,Rhode Island:American Mathematical Society,1984.
Memo
- Memo:
- -