|Table of Contents|

Large Time Behavior to a Chemotaxis-Haptotaxis Model with Nonlinear Diffusion(PDF)

《南京师大学报（自然科学版）》[ISSN:1001-4616/CN:32-1239/N]

Issue:
2023年04期
Page:
17-20
Research Field:
数学
Publishing date:

Info

Title:
Large Time Behavior to a Chemotaxis-Haptotaxis Model with Nonlinear Diffusion
Author(s):
Liu Jintao; Jia Zhe
(School of Mathematics and Statistics,Linyi University,Linyi 276005,China)
Keywords:
chemotaxis-haptotaxis;  nonlinear diffusion;  large time behavior;  energy functional
PACS:
O175.26
DOI:
10.3969/j.issn.1001-4616.2023.04.004
Abstract:
This paper deals with the following chemotaxis-haptotaxis model

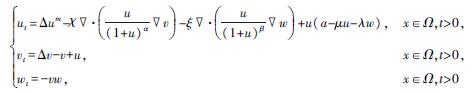
under homogenous Neumann boundary condition in a bounded domain ΩR3. It is shown that when 0<m≤1,for appropriately large μ,the corresponding solution(u,v,w)goes to the steady state (a/μ,a/μ,0) by constructing an appropriate energy functional.

References:

[1]CHAPLAIN M,LOLAS G. Mathematical modelling of cancer invasion of tissue:dynamic heterogeneity[J]. Networks and heterogen media,2016(1):399-439.
[2]ZHENG J,KE Y. Large time behavior of solutions to a fully parabolic chemotaxis-haptotaxis model in mensions[J]. Journal of differential equations,2019,266:1969-2018.
[3]XU H,ZHANG L,JIN C. Global solvability and large time behavior to a chemotaxis-haptotaxis model with nonlinear diffusion[J]. Nonlinear analysis:real world applications,2019,46:238-256.
[4]JIA Z,YANG Z D. Global boundedness to a chemotaxis-haptotaxis model with nonlinear diffusion[J]. Applied mathematics letters,2020,103:106192.
[5]JIA Z,YANG Z D. Global boundedness in a chemotaxis-haptotaxis model with nonlinear diffusion and signal production[J]. Acta mathematic scientia,2021,41A(5):1382-1395.
[6]JIN C. Large time behavior of solutions to a chemotaxis model with porous medium diffusion[J]. Journal of mathematical analysis and applications,2019,478:195-211.
[7]TAO Y,WINKLER M. Large time behavior in a multidimensional chemotaxis-hapotaxis model with slow signal diffusion[J]. SIAM journal on mathematical analysis,2015,47:4229-4250.
[8]TAO Y. Boundedness in a two-dimensional chemotaxis-haptotaxis system[J]. arXiv:1407.7382,2014.
[9]JIN C. Boundedness and global solvability to a chemotaxis-haptotaxis model with slow and fast diffusion[J].Discrete and continuous dynamical systems,2018,23(4):1675-1688.
[10]LI Y,LANKEIT J. Boundedness in a chemotaxis-haptotaxis model with nonlinear diffusion[J]. Nonlinearity,2016,29:1564-1595.

Memo

Memo:
-
Last Update: 2023-12-15